在位操作（Bit Manipulation）的领域里，有一些技巧因其简洁和高效，常常被称作「魔法」。Kernighan’s Algorithm 就是其中最令人印象深刻的一个。

它旨在解决一个经典问题：Population Count（又称 Hamming Weight），即：

如何高效地计算一个整数的二进制表示中，有多少个 1？

0x01 朴素解法的局限

最直观的解法是逐位检查。我们通过循环和移位，依次判断每一位是否为 1。

1
2
3
4
5
6
7
8
9

func hammingWeight(n uint32) int {
    count := 0
    for i := 0; i < 32; i++ {
        if (n & (1 << i)) != 0 {
            count++
        }
    }
    return count
}

这种方法的缺点显而易见：它的执行时间固定为 $O(n)$（$n$ 为整数的位数，如 32）。无论这个数是 0 还是 0xFFFFFFFF，它都必须跑完所有循环。即便数字里只有一个 1，我们也浪费了 31 次循环在检查 0 上。

0x02 核心洞察：精准消除

Kernighan’s Algorithm 的核心思想非常性感：跳过所有的 0，每次循环只处理（并消除）一个 1。

实现这一目标的「魔法指令」只有一行：

1

n = n & (n - 1)

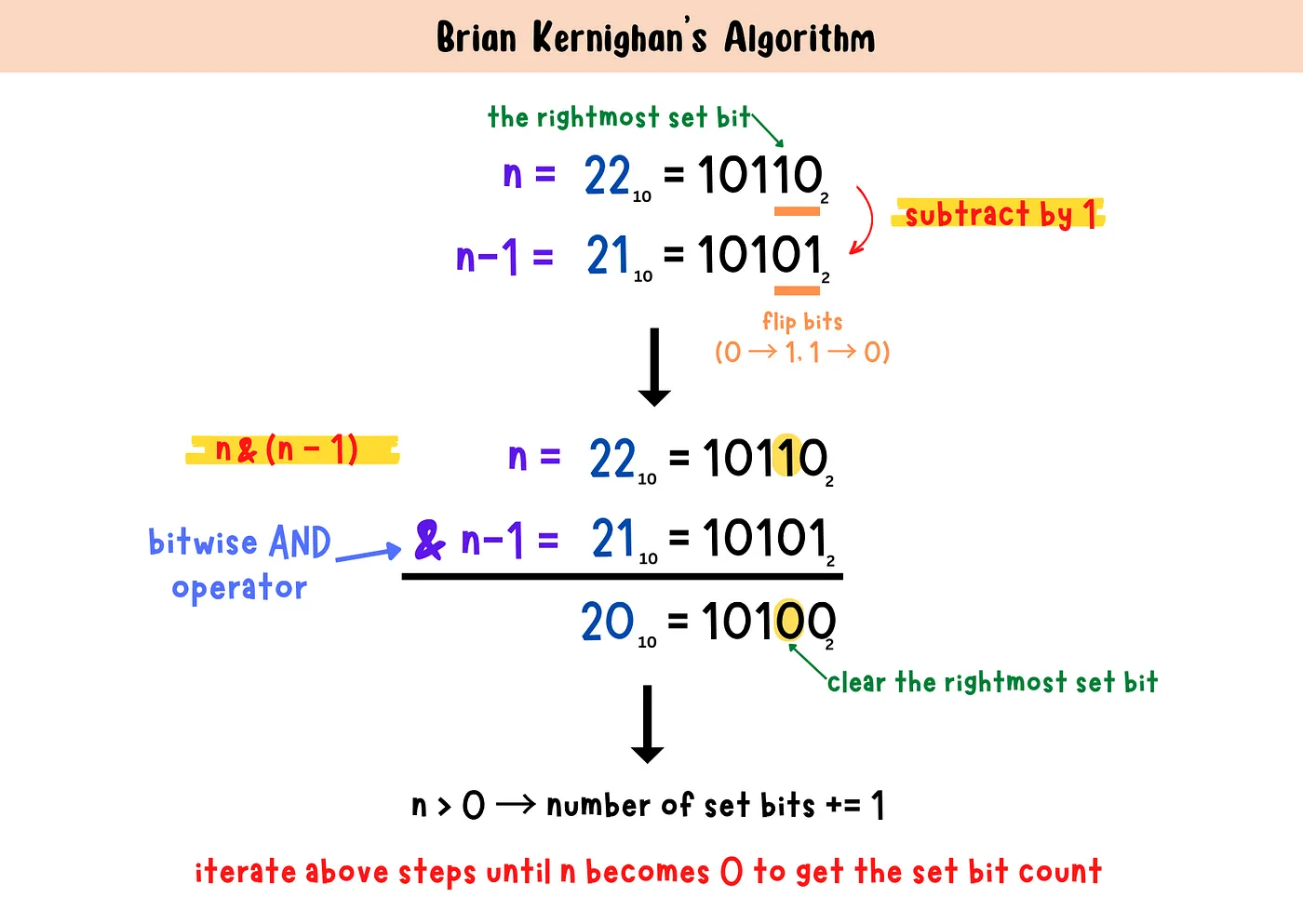
这一行代码的作用是：将 n 的二进制表示中，最右侧的那个 1 (The Rightmost Set Bit) 变为 0，而保持其他位不变。

为什么是 n & (n - 1)？

我们可以将任意整数 $n$ 的二进制结构拆解为三部分：

  1. 高位部分：最右侧 1 左边的所有位。
  2. 关键位：最右侧的那个 1。
  3. 低位部分：关键位右边的所有 0。

即：$n = (\dots\text{High}\dots) \ \mathbf{1} \ (\dots000\dots)$

当我们执行 n - 1 时，借位操作会从最低位一直向左传导，直到遇到那个关键位 1：

  1. 关键位：被「借位」变成了 0。
  2. 低位部分：因为借位，原来的 000... 全部翻转成了 111...。
  3. 高位部分：不受借位影响，保持不变。

现在，我们将 n 与 n - 1 进行 按位与 (&) 操作：

$$ \begin{array}{rcccc} n & = & \text{High} & \mathbf{1} & 00\dots0 \\ n - 1 & = & \text{High} & \mathbf{0} & 11\dots1 \\ \hline \text{Result} & = & \text{High} & \mathbf{0} & 00\dots0 \end{array} $$

结论：高位保持不变，低位全部归零，唯独最右侧的那个 1 被消除了。

0x03 算法演示

在下方输入任意数字（0-255），观察每次迭代如何精准地摘除一个 set bit。

数值:
慢 快
n
n - 1
n & (n-1)
等待开始...
当前 n (十进制): -
已找到 1 的个数: 0
(算法迭代次数): 0
function kernighan(n) {
let count = 0;
while (n > 0) {
// 核心: n-1 翻转最右侧的 1
// 与操作后，该位被消除
n = n & (n - 1);
count++;
}
return count;
}

0x04 复杂度分析

这是 Kernighan’s Algorithm 能够成为经典的原因：

特性朴素解法Kernighan’s Algorithm
循环次数固定 $N$ 次 (32/64)$k$ 次 ($k$ 为 1 的个数)
时间复杂度$O(N)$$O(k)$
优势场景密集型 (全是 1)稀疏型 (1 很少)

在实际应用中，绝大多数整数的 1 都是稀疏分布的。例如对于一个32位整数，如果它只有 3 个 1，该算法只需要运行 3 次循环，性能提升了 10 倍以上。

0x05 代码实现 (Go)

利用这一特性，我们可以写出极简的计数代码。注意循环条件是 n != 0，这意味着一旦所有的 1 被消除，循环立即终止。

1
2
3
4
5
6
7
8

func hammingWeight(n uint32) int {
    count := 0
    for n != 0 {
        n &= (n - 1)  // 消除最右侧的 1
        count++
    }
    return count
}

其逻辑流程如下图所示：

  graph TD
    Start((开始)) --> Cond{n != 0 ?}
    Cond -- Yes --> Step1["n = n & (n - 1)<br>(消除最右侧 1)"]
    Step1 --> Step2[count++]
    Step2 --> Cond
    Cond -- No --> End((返回 count))

    style Step1 fill:#f9f,stroke:#333,stroke-width:2px

0x06 举一反三：更多应用场景

理解了 n & (n - 1) 的本质，我们还可以用它解决更多问题：

1. 判断 2 的幂 (Power of Two)

2 的幂有一个特征：二进制表示中有且仅有一个 1。 这意味着，如果我们消除掉这唯一的 1，结果应该变为 0。

1
2
3
4
5

func isPowerOfTwo(n int) bool {
    // n > 0 排除负数和 0
    // (n & (n - 1)) == 0 说明消除一个 1 后就没了
    return n > 0 && (n & (n - 1)) == 0
}

2. 汉明距离 (Hamming Distance)

汉明距离定义为两个数二进制位不同的个数。 我们只需要先做异或 xor = x ^ y（不同的位变为 1），然后对 xor 应用 Kernighan’s Algorithm 即可。

3. 稀疏位图迭代

在处理 BitMap 或 FlagSet 时，如果我们需要遍历所有被置位的标志，使用此算法可以直接跳跃到下一个置位点，而不需要逐个检查每一位，在大规模稀疏数据处理中效率极高。

0x07 总结

虽然在现代 CPU 指令集（如 x86 的 POPCNT）支持下，硬件级的位计数可以达到单指令周期完成，但 Kernighan’s Algorithm 依然是算法面试和跨平台软件实现中的最优解。它展示了位操作最迷人的一面：通过对二进制微观结构的深刻理解，换取宏观性能的极致优化。

相关题目